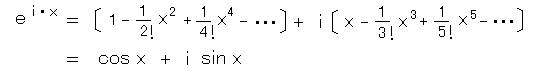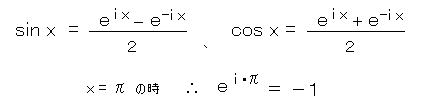　　２．　不変なもの、永遠に続くもの：

　　　　　・・・・・　　「初めにことばがあった。ことばは神と共にあった。ことばは神であった。」（ヨハネ１：１）

　　（１）　自然対数の底　ｅ　の定義：　　（→　（参考）　数学思索の構造２．自然対数の底ｅの定義）

　　　　・・・ｅはその名のとおり、”自然”対数の底（てい）。 ”名”は本質をあらわします（＊）。　指数関数ｅ^ｘ（ｅｘｐｘ　とも表記）の逆関数は ”対数関数”で、（数学ではそのまま）ｌｏｇｘ、（物理・工学では常用対数ｌｏｇ_１０ｘと区別されるために）　ｌｎｘ　と表記されます。これは、自然を描写するのにあまりにも普遍的に用いられるので、このように省略されます。
　　　・・・　”自然対数”の”底”についての指数関数という、”バカボン”の”パパ”的な命名法！これでｅのだ！　「主」についても、「アブラハム、イサク、ヤコブの神」と言う。

　　では、自然対数の底ｅ の一般的な定義から、その素性を調べてみましょう。（＊　解析学は、”変化”の思索です）
　　定義式は、　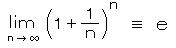　　　です。　この左辺（ｌｉｍｎ→∞ は、ｎが無限大になるまでの極限（ｌｉｍｉｔ）にもっていくという意味）に、自然数　ｎ＝１、２、３、・・・を代入して、

ｎ	１	２	３	・・・	１０	１００	１０００	１００００	・・・	∞
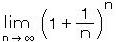	２	２．２５	２．３７０・・・	・・・	２．５９３７・・・	２．７０４８１・・・	２．７１６９２３９・・・	２．７１８１４５９２６・・・	・・・	２．７１８２８１８２８４５９０４５２３５３６０２８７４７１３５２・・・

　　このように、ｎが大きくなると、無限に続くある一定の値（２．７１８２８１８２８４５９０４５２３５３６０２８７４７１３５２・・・、フナ一箸二箸　一箸二箸　しごくおしい、と憶える）に収束していきます。この極限値を、ｅ　と定義します。（このｅは、円周率π のように無理数であり、超越数でもあります。）

　　収束する極限を持つ数列は他にもさまざまなものがありますが、このｅがいかに特別なものであるかを見ていきましょう。

　　（２）　繰り返し微分しても変わらない関数：

　　微分とは、関数ｆ（ｘ）の変化率の関数（＝導関数）のことを言います。導関数の定義は、
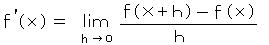　　　　　　で与えられます。
　　これは、ｘの値をほんの少しｈだけ変えてやると、ｆ（ｘ）がどのくらい変わるか、という意味です。図形で表現するならば、ｙ＝ｆ（ｘ）　の曲線に対して、そのｘのときの接点の勾配になります。

　　ここで、何度微分しても変わらない
　　　　　　　　　　　　　　　　　　　　ｆ（ｘ）　＝　ｆ ’（ｘ）　＝　ｆ ’’（ｘ）　＝　・・・・　　
となるような関数　ｆ（ｘ）　＝　ａ^ｘ　を考えましょう。
　　この何度微分しても変わらないことは、　　ｆ（ｘ）　＝　ｆ ’（ｘ）　　　　が示されれば十分です。

　　導関数の定義より、　　（ａ^ｘ）’　＝　ｌｉｍ _{ｈ → ０} （ａ^ｘ＋ｈ－ａ^ｘ）/ ｈ
　　これを分離して、　　　　　　　　　＝　ａ^ｘ・ｌｉｍ _{ｈ → ０} （ａ^ｈ－１）/ ｈ
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　＊　この分離するところで、定義式のｌｉｍ_ｎ→∞ （１＋（１/ｎ））^ｎの形の元が出来上がる

　　この右辺と左辺を比較して、　（ａ^ｘ）’　＝　ａ^ｘ　　となるためには、　　　でなければならず、これを満たすａを　ｅ、
　　すなわち、　　　ｆ（ｘ）　＝　ｅ^ｘ　　とおきます。

　　では、このｅがどのような形であるかを導きます。　この式を変形すると、
　　　　ｌｉｍ _{ｈ → ０} （ｅ^ｈ－１）/ ｈ　＝　ｌｉｍ _{ｈ → ０} ｈ、　　　ｌｉｍ _{ｈ → ０} ｅ^ｈ　＝　ｌｉｍ _{ｈ → ０} （ｈ＋１）
　　　　両辺を　ｌｉｍ _{ｈ → ＋０} １ / ｈ乗すると　（　ｌｉｍ _{ｈ → －０} １ / ｈ乗　でも同じ）、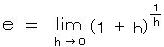　　

　　ｈ＝１/ｎ　（ｎ＞０　の整数）とおけば、　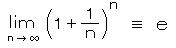　　、　すなわち、ｅ　の定義式が導かれ、このｅ　は自然対数の底であることが証明されました。

　　したがって、指数関数ｅ^ｘは、　ｅ^ｘ　＝　（ｅ^ｘ）’　＝　（ｅ^ｘ）’’　＝　（ｅ^ｘ）’’’　＝　・・・・　　となって、何回微分しても関数の形が変わらない関数であることが分かります。
　　（・・・　他にも証明法はいくつかあります。対数関数を使って導くのが一般的です。）

　　また、微分の逆の積分（不定積分、積分定数を省略）も、　　ｅ^ｘ　＝　∫ｅ^ｘｄｘ　＝　∫（∫ｅ^ｘｄｘ）ｄｘ　＝　・・・・　　となって、何回積分しても形が変わらないことが証明されています。
　　　　　　　・・・・　∫ は ”インテグラル”で積分の記号：　インテグラ（ホンダ、９０年代）は、天皇陛下の愛車です？

　　たとえば、電磁波（＝　赤外線、光、紫外線、Ｘ線、ガンマ線などを含む）の進行は、電場の変化が直交して磁場の変化に伝わり、その磁場に変化が直交して電場の変化になって伝わる、という伝播を光の速さで繰り返します。このとき、微分（あるいは積分）を無限に繰り返していきます。

　　
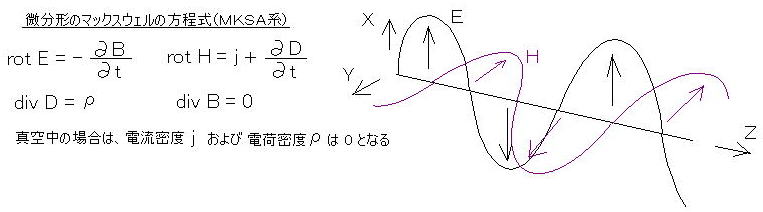
　　真空には 電磁誘導の性質があって、初めに電場の変化があったとすると、　電場の変化　→　磁場の変化　→　－側の電場の変化　→　－側の磁場の変化　→　（元の）電場の変化　→　・・・　　というように、４サイクルで変化が伝播していきます。このようなバネの復元力のような性質は２つあって、誘電率 ε₀　と透磁率 μ₀　が真空の性質として備えられています。伝播の速さは、√（ε₀・μ₀）＝ｃ（光速）であって、電磁波、Ｘ線、γ線などは光と同じもの（振動周波数が異なるだけ）であることが証明されています。

　　　　・・・・・　　　「このことばにはいのちがあった。このいのちは、人の光であった。」（ヨハネ１：４）

　　（３）　自然における永続性：

　　さて、長々と高校数学レベルのことを記述してきましたが、この指数関数　ｅ^ｘ　（単に指数関数と呼ぶ）は、微分方程式の解になるなど、数学、物理に非常に応用範囲が広く、自然の性質の大部分を記述することができます。

　　物理や工学では、それぞれの物理法則に基づいて、それぞれの理論の出発点となる微分方程式が構築されるのが普通で、その解は、大体 指数関数を基本とする形になります。

　　たとえば、電気回路の分野で、

　　１）　　ファラデーの法則、オームの法則をあわせて、　それを直列につないだ回路では、１次微分方程式となり、

　　　　　　　　　　　　　　　　　　ｄＶ/ｄｔ　＝　－Ｖ/ＲＣ　　　　となり、その解は、変数分離形　　ｄＶ/Ｖ　＝　－ｄｔ/ＲＣ　　の両辺を積分して、
　　　　　　　　　　　　　　　　　　　　ｌｎＶ　＝　－ｔ/ＲＣ　＋　ｃｏｎｓｔ　　　　　　　∴　　　Ｖ　＝　Ｖ₀ｅ^{－ｔ/ＲＣ}
　　電流ｉであらわすと、　　ｉ　＝　Ｖ / Ｒ　より、　　　　　　　　　　　　　　　　　　　　　ｉ　＝　Ｉ₀ｅ^{－ｔ/ＲＣ}　　・・・・　①
　　これは、時間ｔの経過に対する減衰曲線になります。（↓　下図右上）

　　２）　　ファラデーの法則、ヘンリーの法則、オームの法則をあわせて、　それを直列につないだ回路では、２次微分方程式となり、

　　　　　　　　　　　　　　　　　　　（電荷解法）　

　　これは境界条件によって解が異なります。抵抗Ｒが無視できる場合（Ｒ＝０）は、１次の項は消え振動項のみとなり、比較的簡単に解けます。（＊　Ｒが０でない場合は、減衰項と振動項の積の形（＝減衰振動）になり、解法は複雑です。　→　３．電磁場の直交性）
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　ｑ　＝　Ｑ₀ ｓｉｎ（ωｔ＋ α₀）
　　電流ｉであらわすと、　ｉ　＝　－ｄｑ / ｄｔ　より、　　　　　　　ｉ　＝　－Ｉ₀ ｃｏｓ（ωｔ＋ α₀）　　・・・　α₀：　位相　　・・・・　②
の形になり、これは周期現象を表す式になっています。
　　周期現象なので、その振動の周波数が存在し、　　　　　　　ｆ　＝　ω/２π　＝　１/（２π√（ＬＣ））　　　　・・・・　③

　　　　

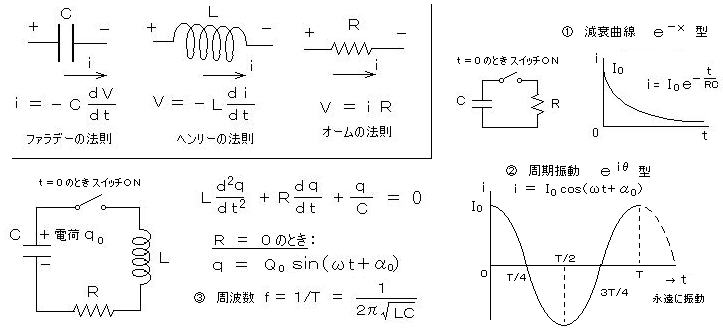
　　この　① が、　だらだらと減少する減衰曲線、　　・・・・　　いわば、”死”の曲線：　　ｅ^－ｘ型
　　　　　② が、　永続的振動を与える調和振動の曲線　　・・・　いわば、”いのち”の曲線：　　ｅ^ｉθ 型
をそれぞれ表します。
　　すべての振動波形は、ｓｉｎ曲線（三角関数）の重ね合わせで表現されます。（＝フーリエ級数）
　　（ただし、実際の回路では、インダクタンス（Ｌ）に抵抗成分（Ｒ）が含まれるので ”減衰振動”の形になり、”死”と”いのち”が入り混じった構造になっています。）

　　前節で述べたとおり、他の物理現象でも同様に分類されます。
　　　　１）　ｅ^－^ｘ 型（死のパターン）：　熱力学、統計力学、梁のたわみ、砂利の山の形、コンデンサーの充・放電、放射性核の崩壊、・・・
　　　　２）　ｅ^ｉθ 型（いのちのパターン）：　周期現象、振動・波動、光学、発振、電磁波、量子力学的振動、・・・

　　（４）　指数関数の展開とオイラーの恒等式：

　　この解に現れる、　ｓｉｎｘ、　ｃｏｓｘは、虚数を冪（べき）とするｅの指数関数であって、　ｅ^ｉθ　の形をとり、整式に展開すると、
　　　　　　　　　　　　　　　
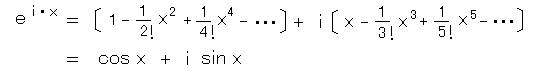
　　虚数冪の指数関数は、このように 無限級数に虚数値を代入することで定義されます。
　　この式を書き直すと、
　　　　　　　　　　　　　　　　
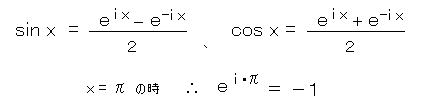
という、驚くべき関係が出てきます。
　　この、知る人ぞ知る、　　　ｅ ^{ｉ π}　＝　－１　　　　（オイラーの恒等式）　　　こそ、思索の３大分野のそれぞれの数学定数（幾何学の π、代数学のｉ、解析学のｅ）が一点に集まった、数学史上最もエレガントな式になっています。（　→　次項）

　　＊　名は本質をあらわす：　　聖書の人物名にはヘブライ語の意味があります。

　　　　　ｅｘ）　ヨハネ：主は恵み深い、　ペテロ：岩（← シモン：葦）、　マタイ：主の贈り物、　パウロ（← サウロ、サウル）：小さい、　ダニエル：神は審判者、　イザヤ：主は救い、　エレミヤ：主は高める、　エゼキエル：神が強くする、　エノク（ハノク、ハヌカ）：捧げ物、　ヨセフ：増加の祝福、　マナセ：忘れる、　ベニヤミン：右手の息子、　モーセ：引き出す、　エリヤ：ヤハウエは神、　・・・。
　　イエス様は、イェホーシュア（イエスースはギリシャ語）、　ホセア：「救い」、　ヨシュア：主は救い、（ホセア→ヨシュア→イェホーシュア（短縮形：イエシュワー）＝イエス）
　　キリスト（キストス（ギ））とは、「油注がれた者」（メシヤ、油を注ぐのは旧約時代の「王」を任命するときの儀式、油＝聖霊）。
　　当時 ”イエス”はありふれた名前だったので「ナザレのイエス」という呼び方で区別しました。しかし、その本質の呼び名は、イザヤ書で言っています。
　　　　　　　　　　　　「不思議な助言者、力ある神、永遠の父、平和の君」（イザヤ９：６）

　　∴　　「自然対数の底」とは、創造の本質を表すので、「イエス様」の新しい名の一つかも知れませんね。（黙示録３：１２）

　　　　　　　　　（参考）　　　　　　・　聖書人名辞典（旧約）　　　　　　　・　ヘブライ語が起源の名前

　　　　　　　　　　　　　　　　次へ　　　　　　　　　　　　　　トップに戻る